Equazione di Van Deemter

L’equazione di van Deemter in cromatografia, chiamata in questo modo per Jan van Deemter, mette in relazione la varianza per unità di lunghezza di una colonna di separazione con la velocità della fase mobile lineare considerando le proprietà fisiche, cinetiche e termodinamiche di una separazione. Queste proprietà includono percorsi all'interno della colonna, diffusione (assiale e longitudinale) e cinetica di trasferimento di massa tra fasi stazionarie e mobili. Nella cromatografia liquida, la velocità della fase mobile viene presa come velocità di uscita, ovvero il rapporto tra la portata in mL / secondo e l'area della sezione trasversale del "percorso di flusso in uscita dalla colonna". Per una colonna impaccata, l'area della sezione trasversale del percorso del flusso di uscita della colonna viene generalmente presa come 0,6 volte l'area della sezione trasversale della colonna. In alternativa, la velocità lineare può essere considerata come il rapporto tra la lunghezza della colonna e il tempo morto. Se la fase mobile è un gas, è necessario applicare la correzione della pressione. La varianza per unità di lunghezza della colonna viene presa come rapporto tra la lunghezza della colonna e l'efficienza della colonna nei piatti teorici. L'equazione di Van Deemter è una funzione iperbolica che prevede che vi sia una velocità ottimale alla quale ci sarà la varianza minima per unità di lunghezza della colonna e, quindi, la massima efficienza. L'equazione di Van Deemter fu il risultato della prima applicazione della teoria della cinetica al processo di eluizione cromatografica.

Formulazione

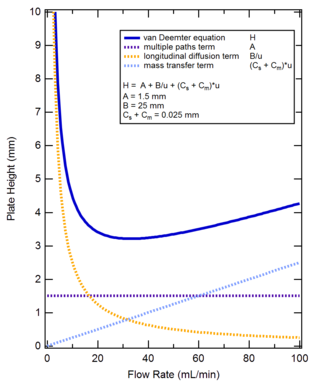
L'equazione di Van Deemter mette in relazione l'altezza equivalente a un piatto teorico (HETP) di una colonna cromatografica al variare dei parametri di flusso e cinetici che causano l'ampliamento del picco, come segue:

$HETP=A+{\frac {B}{u}}+(C_{s}+C_{m})\cdot u$

Dove:

• HETP = una misura del potere risolutivo della colonna [m];
• A = effetto dei percorsi multipli che spiega perché le molecole non giungano al rivelatore tutti insieme ma in tempi diversi per i percorsi diversi percorsi [m];
• B = coefficiente di diffusione delle particelle di eluizione nella direzione longitudinale, con conseguente dispersione [m ² s ⁻¹] cioè contribuisce all'allargamento dei picchi, la direzione è diversa rispetto a quella normale in-let e out-let;
• C = resistenza al coefficiente di trasferimento di massa dell'analita tra fase mobile e fase stazionaria [s], è il fattore dominante nella deformazione del picco, le molecole di soluto in base a dove si trovano possono passare oltre le particelle o possono essere adsorbite, in quest'ultimo caso saranno più ritenute, arriveranno dopo e di conseguenza saranno rivelate in tempi diversi. Ognuno dei tre fattori, soprattutto il terzo, contribuisce alla perdita di efficienza;
• u = velocità lineare [ms ⁻¹].

Nei capillari tubolari aperti, il termine A sarà zero poiché la mancanza di riempimento implica che non si verifichino canalizzazioni. Nelle colonne impaccate, tuttavia, esistono più percorsi distinti ("canali") attraverso il riempimento della colonna, che si traduce nella diffusione della banda. In quest'ultimo caso, A non sarà nullo ma avrà un valore pressoché indipendente da u.

La forma dell'equazione di Van Deemter è tale che l'HETP raggiunge un valore minimo a una determinata velocità del flusso. A questa portata, il potere risolutivo della colonna è massimizzato, sebbene in pratica il tempo di eluizione sia probabilmente impraticabile. Differenziando l'equazione di Van Deemter rispetto alla velocità, impostando l'espressione risultante uguale a zero e risolvendo per la velocità ottimale si ottiene quanto segue:

$u={\sqrt {\frac {B}{C}}}$

Conteggio dei piatti teorici

Due picchi ben risolti in un cromatogramma.

L'altezza dei piatti teorici è indicata come:

$H={\frac {L}{N}}\,$

con $L\,$ la lunghezza della colonna e $N\,$ il numero di piastre teoriche può essere stimato da un cromatogramma mediante analisi del tempo di ritenzione $t_{R}\,$ per ogni componente e la sua deviazione standard $\sigma \,$ come misura della larghezza del picco, a condizione che la curva di eluizione rappresenti una curva gaussiana.

In questo caso il conteggio delle piastre è dato da:

$N=\left({\frac {t_{R}}{\sigma }}\right)^{2}\,$

Utilizzando la larghezza del picco a mezza altezza $W_{1/2}$, l'equazione è:

$N=8\ln(2)\cdot \left({\frac {t_{R}}{W_{1/2}}}\right)^{2}\,$

o con la larghezza alla base del picco:

$N=16\cdot \left({\frac {t_{R}}{W_{base}}}\right)^{2}\,$

Van Deemter ampliato

L'equazione di Van Deemter può essere ulteriormente estesa a:

$H=2\lambda d_{p}+{2\gamma D_{m} \over u}+{\omega (d_{p}{\mbox{ or }}d_{c})^{2}u \over D_{m}}+{Rd_{f}^{2}u \over D_{s}}$

Dove:

• H è il numero di piatti teorici
• λ è la forma delle particelle (per quanto riguarda l'imballaggio)
• d _p è il diametro delle particelle
• γ, ω e R sono costanti
• D _m è il coefficiente di diffusione della fase mobile
• d _c è il diametro capillare
• d _f è lo spessore del film
• D _s è il coefficiente di diffusione della fase stazionaria
• u è la velocità lineare

Equazione di Rodrigues

L’equazione di Rodrigues, chiamata per Alírio Rodrigues, è un'estensione dell'equazione di Van Deemter usata per descrivere l'efficienza di un letto di particelle permeabili (pori grandi).

L'equazione è:

$HETP=A+{\frac {B}{u}}+C\cdot f(\lambda )\cdot u$

Dove:

$f(\lambda )={\frac {3}{\lambda }}\left[{\frac {1}{\tanh(\lambda )}}-{\frac {1}{\lambda }}\right]$

e $\lambda$ è il numero di Péclet intraparticolare.