Momento torcente
Il momento torcente, (in inglese twisting moment o twisting couple) [1] in meccanica, indica un momento meccanico applicato perpendicolarmente a due facce opposte rispetto ad una sezione qualsiasi. Il caso di carico in cui si manifesta è detta torsione: se non ci sono altre sollecitazioni si parla di torsione pura.
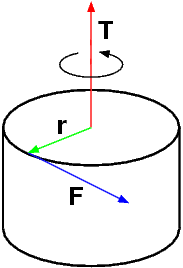
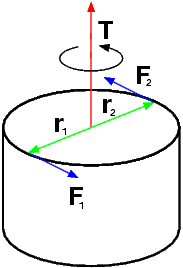
Nel caso non vi siano altri tipi di sollecitazione, ciascuno dei due momenti è una coppia di forze, in quanto è equivalente all'applicazione di due forze distinte uguali e contrarie, ciascuna con modulo pari al rapporto tra il modulo del momento torcente e la distanza tra le loro rette d'azione, e agenti su due punti esattamente opposti rispetto al suo fulcro.
Definizione
modificaSi può definire momento torcente il momento meccanico normale ad una sezione capace di produrvi una tensione. L'effetto prodotto dal momento torcente non è quindi di imprimere una rotazione della leva intorno al fulcro, che compete invece al momento trasmesso dalla sezione, ovvero alla differenza tra il momento meccanico perpendicolare agente sulla sezione e quello torcente dissipato nella sezione.
Matematicamente si ha:
dove:
- M è la coppia motrice perpendicolare.
- M0 è la coppia resistente perpendicolare.
- ΔM è il momento torcente.
L'unità di misura del momento torcente naturalmente sarà quella del momento meccanico, quindi nel Sistema internazionale di unità di misura il newton metro (N·m).
Tensione associata
modificaIl momento torcente in un qualsiasi corpo continuo produce uno sforzo di taglio ( chiamato anche "tensione di taglio" ).
Energia di deformazione elastica
modificaL'energia di deformazione associata alla torsione in un solido elastico vale:
Applicazioni ed esempi
modificaIn un autoveicolo alla coppia motrice impressa dal differenziale automobilistico a un capo di un semiasse corrisponde una coppia resistente della ruota all'altro estremo che può essere diversa e variabile con l'attrito ruota-terreno. A ruota libera (in pratica come quando nel fango non fa presa) tutta la ruota accelera velocemente e non vi è teoricamente momento torcente; quando questa è completamente bloccata invece tutta la coppia motrice viene equilibrata a fine semiasse da una coppia resistente quindi tutta la coppia motrice si traduce in un momento torcente: dando gas al motore questo cresce finché o si supera il vincolo o si rompe il semiasse. In pratica, anche a ruota libera i bassi attriti dei cuscinetti portanti del semiasse determinano un piccolo momento resistente che si accoppia con una parte uguale di momento agente a dare il momento torcente; la coppia che accelera lo sterzo è la parte rimanente della coppia motrice e quindi l'accelerazione angolare è leggermente minore di quella data dalla coppia trasmessa dal differenziale.
Di tipo torcente è poi anche la coppia motrice lungo l'asse dello sterzo imposta dal guidatore sul volante quando questo è bloccato, non quando è completamente libero di girare, perché nel primo caso la coppia motrice è equilibrata dal momento resistente del bloccasterzo applicato alla base e determina una tensione di taglio nell'albero dello sterzo; nel secondo invece in assenza di coppia resistente la coppia motrice si traduce tutta in una accelerazione angolare dello sterzo.
Questi esempi servono a chiarire che il momento torcente come gli altri tipi di sorgenti di tensione non si manifestano solo in statica, ovvero con corpi fermi o in rotazione-traslazione costanti nel tempo per un sistema inerziale come la trave di una struttura, ma anche in un moto accelerato qualsiasi. Inoltre poiché nel funzionamento stazionario di un rotore coppia motrice e coppia resistente sono uguali fra loro e uguali al momento torcente, e poiché l'attrito coi cuscinetti e il fluido circostante (a meno che il rotore non sia sospeso nel vuoto assoluto) aumenta sempre con la velocità angolare, esiste sempre un limite strutturale alla velocità angolare del rotore che corrisponde al momento torcente di rottura, che naturalmente è tanto più restrittivo quanto più alto è l'attrito.
Analogia fluidodinamica
modificaLa comprensione intuitiva dell'andamento delle tensioni generate da un momento torcente in un solido può risultare poco immediata. Per questo motivo può essere molto utile evidenziarne l'analogia coll'andamento della velocità in una sezione fluida le cui pareti laterali siano in rotazione rispetto all'asse baricentrico. Si può dimostrare che le equazioni che reggono il problema idrodinamico descritto sono formalmente identiche a quelle della torsione: l'unica differenza tra le due serie di equazioni, infatti, sono che nella prima compaiono le componenti della velocità del fluido nel punto e nella seconda le componenti della tensione tangenziale nel medesimo punto.
Per effetto di questa differenza di rotazione, il liquido all'interno avrà in ogni punto delle velocità differenti sia per modulo che per direzione. Tale analogia, tuttavia, non semplifica la soluzione del problema della torsione dal momento che le difficoltà analitiche sono uguali a quelle del caso fluidodinamico.
Scienza delle costruzioni
modificaNella scienza delle costruzioni si utilizza il momento torcente per calcolare gli sforzi che avvengono durante la torsione di un qualsiasi profilo. Generalmente si considera il momento applicato nel baricentro della sezione; se ciò non avviene, la soluzione al problema dell'equilibrio elastico in termini di spostamenti comporta solo l'aggiunta di un moto rigido, mentre la soluzione in termini di tensioni risulta invariata. Si dimostra che il moto rigido è mediamente nullo sulla trave se il momento torcente è applicato nel centro di torsione della sezione[2].
La torsione può essere causata anche dall'applicazione di una forza di taglio eccentrica rispetto al centro di taglio: in tal caso si può scomporre la sollecitazione risultante nelle due sollecitazioni semplici di taglio puro e torsione pura, considerando il sistema di forze equivalente costituito dalla forza di medesimo modulo trasportata parallelamente a sé stessa fino ad avere retta d'azione passante per il suddetto punto e da un momento torcente di trasporto.
Note
modificaVoci correlate
modificaCollegamenti esterni
modifica- (EN) couple, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.