Superformula
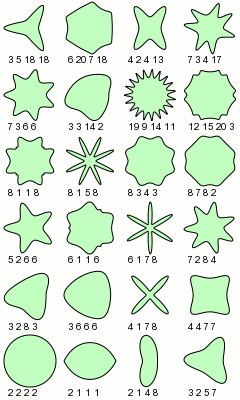
La superformula è una generalizzazione delle funzioni circolari a due dimensioni in coordinate polari, che permette tramite pochi parametri di ricavare moltissime forme geometriche, dette superforme.
L'equazione della superformula è
dove e sono le coordinate polari, sono numeri reali, e sono numeri reali non nulli.
Fu pubblicata per la prima volta nell'aprile del 2003 dal biologo Johan Gielis sul numero 90 dell'American Journal of Botany. Deriva da una generalizzazione della superellisse del matematico danese Piet Hein.
Estensione a dimensioni superiori
modificaPer estendere a 3, 4 o dimensioni, basta moltiplicare più superforme tra loro. Ecco alcuni esempi in tre dimensioni, ottenuti tramite il prodotto sferico di due superformule e , definito da:
dove varia tra e (latitudine) e tra e (longitudine).
| Alcuni esempi di superforme in tre dimensioni. |
Voci correlate
modificaAltri progetti
modifica- Wikimedia Commons contiene immagini o altri file su supershape
Collegamenti esterni
modifica- (EN) Paul Bourke, SuperShapes, su Centre for Astrophysics and Supercomputing, Swinburne Universe of Technology, marzo 2002 (archiviato dall'url originale il 18 aprile 2003).
- SuperForm-ula da una unica funzione polare un incredibile numero di forme geometriche!, su users.quipo.it. URL consultato il 22 febbraio 2023.
- La natura in una superformula, su galileonet.it. URL consultato il 22 febbraio 2023.
- La “superformula” che simula la natura, su lescienze.it. URL consultato il 22 febbraio 2023.
![{\displaystyle {\frac {1}{\rho }}={\sqrt[{n_{1}}]{\left|{\frac {1}{a}}\cos \left({\frac {m}{4}}\phi \right)\right|^{n_{2}}+\left|{\frac {1}{b}}\sin \left({\frac {m}{4}}\phi \right)\right|^{n_{3}}}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd58824285efaad3b310570a1316ea9ad1b42b52)




