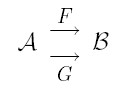Trasformazione naturale
In teoria delle categorie una trasformazione naturale è una freccia tra funtori "paralleli".
che rende possibile definire la categoria di tutti i funtori
tra due categorie assegnate.
Definizione
modificaSiano
due funtori tra le categorie e .
Una trasformazione naturale è una collezione
di frecce di indicizzate dagli oggetti di e tale che il seguente diagramma commuta per ogni freccia di :
cioè .
Composizione orizzontale
modificaSiano date le trasformazioni naturali
ove sono funtori tra due categorie , mentre sono funtori tra due categorie .
Se ne può definire la composizione orizzontale
come quella trasformazione naturale le cui frecce, nella categoria , siano definite in uno dei due modi equivalenti:
,
.
infatti, applicando i funtori H,K al diagramma della trasformazione naturale tra F e G otteniamo:
Composizione verticale
modificaSiano date le trasformazioni naturali
ove sono funtori tra due categorie .
Se ne può definire la composizione verticale
come quella trasformazione naturale le cui frecce, nella categoria , siano definite nel modo elementare:
Categoria dei funtori
modificaSiamo ora pronti per definire la categoria dei funtori come quella categoria che ha per oggetti tutti i funtori , per frecce le trasformazioni naturali tra tali funtori e la composizione di frecce sia proprio la composizione verticale poc'anzi definita.
Esempio 1
Se è la categoria degli insiemi e è la categoria duale di una categoria ( è ottenuta invertendo tutte le frecce di ), allora la categoria è la categoria dei prefasci su .
Esempio 2
Sia la categoria con due oggetti distinti e una sola freccia tra essi. Sia l'insieme ordinato dei numeri razionali visto come categoria ponendo i numeri come oggetti e le relazioni come frecce .
Si verifica che i funtori sono le sezioni di numeri razionali (con l'aggiunta dell'insieme vuoto e dell'intero ). Quindi abbiamo la formula notevole:
ove è l'insieme ordinato dei numeri reali con l'aggiunta di e .
Bibliografia
modifica- Saunders Mac Lane, Categorie nella pratica matematica, Editore Boringhieri, 1977.