Esagono magico
Un esagono magico di ordine n è una disposizione di numeri tra loro distinti in una tabella esagonale composta da n celle per ogni lato, in modo che la somma dei numeri in ogni riga, in ciascuna delle tre direzioni possibili, abbia come somma la stessa costante magica. Un esagono magico normale ha il vincolo ulteriore di usare gli interi consecutivi da 1 a 3n² − 3n + 1. Si può dimostrare che esistono esagoni magici normali solo per n = 1 (banale) e n = 3; inoltre, la soluzione di ordine 3 è essenzialmente unica, a meno di rotazioni e riflessioni.

| |
| Ordine 1 M = 1 |
Ordine 3 M = 38 |
L'esagono magico di ordine 3 è stato pubblicato molte volte come una "nuova" scoperta. Il riferimento più antico noto è quello di Ernst von Haselberg, nel 1887.
Anche se non esistono esagoni magici normali di ordine maggiore di 3, è possibile trovare esagoni leggermente "anormali", che cioè contengano sì tutte cifre consecutive, ma non inizino con 1. Ne sono un esempio gli esagoni di ordine 4 e 5 scoperti da Zahray Arsen:
L'esagono di ordine 4 inizia con 3 e termina con 38; la costante magica è 111. Quello di ordine 5 inizia con 6 e termina con 66; la sua costante magica è 244.
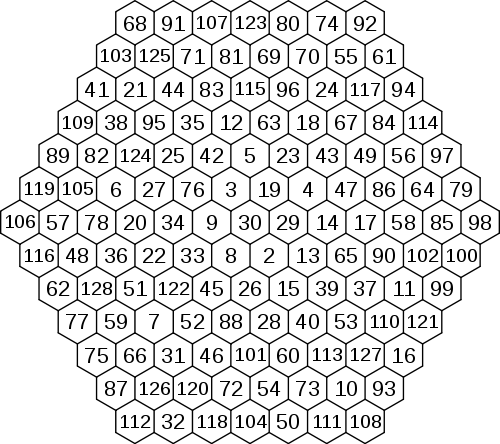
Al momento il più grande esagono magico conosciuto è stato trovato da Zahray Arsen il 22 marzo 2006: inizia con 2 e termina con 128, con una costante magica di 635.
Tuttavia, un esagono magico più grande, ma "diverso (essendo formato da interi opposti)", di ordine 8, è stato creato da Louis K. Hoelbling il 5 febbraio 2006:
Inizia con -84 e termina con 84, e la sua costante magica è 0.
Dimostrazione
modificaEcco una traccia di dimostrazione che non possono esistere esagoni magici di ordine diverso da 1 e 3.
La costante magica M di un esagono magico normale si può determinare come segue. I numeri nell'esagono sono consecutivi, quindi la loro somma è un numero triangolare, per la precisione
Visto che le righe possono essere in tre direzioni, ogni numero è contato tre volte, quindi la somma di tutte le righe è 3s. Ma ci sono r = 3(2n − 1) righe in un esagono, quindi la somma in ogni riga deve essere
Riscrivendo l'espressione come
si vede che 5/(2n − 1) deve essere un intero. Gli unici n ≥ 1 che soddisfano questa condizione sono n = 1 e n = 3.
T-Esagoni Magici
modificaGli esagoni possono essere costruiti anche con triangoli
Esagoni magici di questo tipo possono essere chiamati T-esagoni magici, e presentano molte proprietà in più rispetto agli esagoni magici normali.
Un T-esagono di ordine n è composto da triangoli, e la somma di tutti i suoi numeri è data da
Se decidiamo di costruire un T-esagono, n dev'essere necessariamente pari; infatti, ci sono r = 2n righe in un T-esagono, allora la somma dei numeri di ogni riga dev'essere
Affinché questo sia un intero, n dev'essere pari. Il primo T-esagono, di ordine 2, è stato scoperto da John Baker, il 13 settembre 2003; nel tempo sono stati scoperti T-esagoni di ordine 2, 4, 6 e 8; inoltre, John Baker e David King hanno scoperto che esistono esattamente 59,674,527 T-esagoni di ordine 2 diversi.
Una delle proprietà più sorprendenti dei T-esagoni è che la somma dei numeri contenuti nei triangoli rivolti verso l'alto è uguale alla somma dei numeri contenuti nei triangoli verso il basso; nell'esempio mostrato sopra,
Bibliografia
modifica- Martin Gardner, Enigmi e giochi matematici. Volume quinto, Sansoni, Firenze 1976, pp. 27-30.
Voci correlate
modificaAltri progetti
modifica- Wikimedia Commons contiene immagini o altri file su Esagono magico
Collegamenti esterni
modificaEsagono magico (non normale) di ordine 6, di Louis Hoelbling. Hexagonia