Geometria birazionale
In matematica, la geometria birazionale è un campo appartenente della geometria algebrica il cui obiettivo è determinare se due varietà algebriche sono isomorfe, ad eccezione di un insieme trascurabile.
Applicazioni modifica
Un'applicazione ad esempio è razionale (in) una varietà (assunto irriducibile) X ad un'altra varietà Y, denotato X⇢Y, è definito come un morfismo un non vuoto aperto U di X a Y. U è aperto nel senso della topologia di Zariski e quindi ha come complemento un sottoinsieme di X di dimensione più piccola. In concreto, un'applicazione razionale può essere definita dalle funzioni razionali delle coordinate.
Mappa birazionale modifica
Una mappa birazionale da X a Y è una mappa razionale di tipo tale che esista una mappa YX inversa di f. Una mappa birazionale induce un isomorfismo di una X aperta non vuota a una Y stessa. Diciamo quindi che X e Y sono equivalenti birazionali (o talvolta semplicemente birazionali). In termini algebrici, due varietà su un campo k sono birazionali se e solo se i loro campi di funzione (en) sono isomorfi come estensioni di k.
Morfismo birazionale modifica
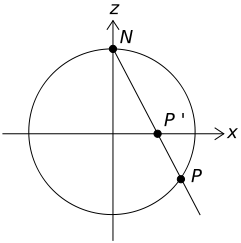
Un caso particolare è quello del termine di morfismo birazionale , vale a dire che f è ovunque definito, ma non necessariamente il suo inverso. Questo si verifica quando f invia alcune sottovarietà X di punti di Y. Una varietà X si dice razionale se è birealmente equivalente a uno spazio affine (o proiettivo), in altre parole se ad eccezione di un sottoinsieme di dimensione minore è identificata con uno spazio affine a un sottospazio di dimensione minore vicino). Ad esempio, il cerchio dell'equazione è una curva razionale, poiché le mappe definiscono una mappa razionale dalla retta al cerchio (eccetto per il punto M (0,-1)) il cui reciproco inviando il punto P (x, y) al punto P' di ascissa
è definito ovunque tranne da M. Le curve razionali sono anche chiamate unicursali. Più in generale, qualsiasi ipersuperficie X non vuota di grado 2 è razionale quadrica, qualunque sia la sua dimensione n; lo dimostriamo utilizzando la proiezione stereografica, definita prendendo p un punto di X, e associando ad ogni punto q di X la retta (p, q) dello spazio proiettivo P n delle rette passanti per p. È un'equivalenza birazionale, ma non un isomorfismo molteplice, perché non è definita in q = p e la mappa inversa non è definita sulle linee di X che contengono p.
Modelli minimi e risoluzione delle singolarità modifica
Ogni varietà algebrica è birazionale per una varietà proiettiva (ad esempio il lemma di Chow). Nel contesto della classificazione birazionale, è generalmente più pratico lavorare solo con varietà proiettive. Un teorema più profondo dovuto a Heisuke Hironaka che riguarda la risoluzione delle singolarità; egli afferma che su un campo di caratteristica zero, qualsiasi varietà è birealmente equivalente a una varietà proiettiva liscia, cioè senza un punto singolare. Se due curve proiettive lisce sono birazionali, sono isomorfe. Questa non ottiene più in dimensioni superiori, grazie alla tecnica dello scoppio, che permette di costruire varietà birealmente equivalenti, ma aventi numeri di Betti differenti. Questo porta alla ricerca di "modelli minimi", vale a dire delle varietà più facili in ciascuna classe di equivalenza birazionale. La definizione rigorosa è che una varietà proiettiva X è minima se il fascio di linee canoniche è di grado positivo su ciascuna curva di X; in altre parole KX è nef.
Questa ricerca è completamente riuscita per le superfici algebriche. La scuola italiana aveva ottenuto intorno al 1900 un risultato a sua volta parte della classificazione di Enriques-Kodaira secondo il quale qualsiasi superficie X è birazionale, cioè ad un prodotto per una certa curva C oppure a una superficie minima Y. I due casi si escludono a vicenda e Y è unico nel secondo caso; Y viene chiamato il modello minimale di X.
Invarianti modifica
Più in generale, è difficile dimostrare che due varietà non sono equivalenti; un approccio ereditato dalla topologia algebrica consiste nel determinare invarianti, cioè numeri o più in generale strutture algebriche più semplici della varietà stessa che sono conservati da mappe birazionali; se due varietà hanno invarianti distinti, allora non sono necessariamente birealmente equivalenti. Tra gli invarianti più utilizzati, i plurigeni sono le dimensioni delle sezioni di potenze tensoriali del fascio canonico, il fascio di linee di n- forme KX=ΩN1. Definiamo per d≥0 il d-esimo plurigene come la dimensione dello spazio vettoriale delle sezioni globali ; dimostriamo che per varietà proiettive lisce sono invarianti birazionali. In particolare, se uno dei non è zero, X non è razionale.