Numero di riproduzione di base

Il numero di riproduzione di base, indicato e conosciuto come R₀ (dizione: erre con zero), indica, in epidemiologia, la potenziale trasmissibilità di una malattia infettiva non controllata. Più precisamente esso rappresenta il numero di nuovi casi sintomatici generati, in media, da un singolo caso durante il proprio periodo infettivo, in una popolazione che altrimenti non sarebbe infetta: esprime quindi il numero atteso di nuove infezioni originatesi da un singolo individuo nel corso del suo intero periodo di infettività, in una popolazione interamente suscettibile all'inizio di una epidemia o in contesti in cui non siano stati presi provvedimenti per limitare il contagio.

Simulazione della trasmissibilità di una epidemia con R₀=2 (Ebola) e con R₀=4 (SARS)

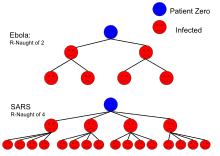
Il concetto trae origine dal tasso netto di riproduzione, utilizzando il termine originario derivato dagli studi demografici; viene anche detto "numero di riproduzione netto" o in certi casi "tasso di riproduzione virale". La definizione del parametro R₀ come metrica nella biologia o epidemiologia matematica non è universalmente condivisa.

Vari studi ritengono improprio l'uso del termine "tasso", in quanto suggerisce una metrica di una quantità in una unità di tempo. Se R₀ fosse un tasso che coinvolge il tempo, fornirebbe informazioni sulla velocità con cui un'epidemia si diffonderà attraverso una popolazione. Ma R₀ non indica se si verificheranno nuovi casi entro 24 ore dal caso iniziale o mesi dopo, proprio come R₀ non indica se la malattia prodotta dall'infezione è grave. L'incoerenza nel nome e nella definizione del parametro R₀ è stata potenzialmente una causa di incomprensione del suo significato.

Storia

Le radici del concetto di riproduzione di base possono essere rintracciate attraverso il lavoro di Ronald Ross, Alfred Lotka e altri, ma la sua prima applicazione moderna in epidemiologia fu di George MacDonald matematico inglese esperto di malattie tropicali nel 1952, che costruì modelli della diffusione della malaria considerando le ondate successive di infezione come generazioni successive nello sviluppo demografico di una popolazione.

La storia del concetto e calcolo del R₀ nel suo passaggio tra le diverse discipline, dalla demografia e ecologia, all'epidemologia, infettivologia e statistica medica non evidenzia una chiara convergenza e oggi sia i modelli di calcolo sia le definizioni possono differire anche notevolmente.

Definizione

Il processo di definizione, calcolo, interpretazione e applicazione di R₀ è tutt'altro che semplice. Sono state proposte numerose definizioni simili ma non identiche.

Dietz afferma che R₀ è "il numero di casi secondari che un caso produrrebbe in una popolazione completamente suscettibile". Fine integra questa definizione con la descrizione "numero medio di casi secondari". Diekmann e colleghi usano la descrizione "numero previsto di casi secondari" e forniscono ulteriore specificità alla terminologia relativa a un singolo caso. Alcune definizioni, come quella del Dipartimento della Salute australiano, aggiungono l'assenza di "qualsiasi intervento deliberato nella trasmissione della malattia".

Il numero di riproduzione di base non deve essere confuso con il numero di riproduzione effettivo R_t o R_e, che è il numero di casi generati nello stato attuale di una popolazione e che dipende dalla frazione (V) di popolazione non suscettibile, cioè immune all’infezione, essendo R_e funzione di R₀(1 – V). Per definizione, R₀ non può essere modificato attraverso campagne di vaccinazione come invece avviene per R. Inoltre è importante notare che sia R sia R₀ sono numeri senza dimensioni e non tassi.

Il numero di riproduzione di base è influenzato da vari fattori, tra i quali la durata del periodo di infettività, la suscettibilità dell'organismo e il numero di individui suscettibili, all'interno della popolazione, coi quali i pazienti infetti entrano in contatto.

Sebbene R₀ rappresenti una realtà biologica, questo valore è generalmente stimato con complessi modelli matematici sviluppati utilizzando varie ipotesi. L'interpretazione delle stime di R₀ derivate da diversi modelli richiede una comprensione delle strutture, degli input e delle interazioni dei modelli. In popolazioni non omogenee il calcolo del R₀ e della dinamica di una epidemia è molto complesso.

Utilizzi

Gli usi più importanti e comuni di R₀ sono: determinare se una malattia infettiva emergente può diffondersi in una popolazione, quale percentuale della popolazione dovrebbe essere immunizzata attraverso la vaccinazione per sradicare una malattia, prevedere quale potrebbe essere il numero di contagiati in una epidemia o la durata della fase espansiva (il periodo tra l'inizio e il picco) dell'epidemia.

Nei modelli di infezione comunemente usati se R₀ < 1, l'infezione sul lungo termine si estinguerà, mentre se R₀ > 1 l'infezione potrà diffondersi nella popolazione. Generalmente, più è alto il valore di R₀, più difficile è controllare l'epidemia.

In un modello semplificato e con un vaccino efficace al 100%, la quota di popolazione che deve essere immune - per precedenti infezioni risolte o per vaccinazione (copertura vaccinale) - per prevenire la diffusione dell'infezione, è data da 1 - 1/R₀.

Più alto è R₀ più alta è la percentuale di popolazione immune per raggiungere l'immunità di gregge.

Al contrario, la proporzione della popolazione che rimane suscettibile alle infezioni nella condizione di equilibrio endemico è 1/R₀.

Variabilità e incertezze del R₀

Stime di R₀

Malattia	Trasmissione	R 0
MERS	Goccioline respiratorie	0,3-0,8
Influenza (ceppi stagionali)	Goccioline respiratorie	0,9–2,1
Influenza suina ( H1N1 del 2009 )	Goccioline respiratorie	1,4–1,6
Influenza spagnola ( H1N1 del 1918 )	Goccioline respiratorie	1,4–2,8
Influenza di Hong Kong ( H3N2 del 1968 )	Goccioline respiratorie	1,1–3,6
Ebola ( epidemia del 2014 )	Fluidi corporei	1,5–2,5
Difterite	Saliva	1,7–4,3
HIV / AIDS	Fluidi corporei	1,09-2,15
SARS	Goccioline respiratorie	2–5
COVID-19	Goccioline respiratorie e aerosol	3,3–5,7
Vaiolo	Goccioline respiratorie	3,5–6
Parotite	Goccioline respiratorie	10-12
Rosolia	Goccioline respiratorie	4,3-9,2
Pertosse	Goccioline respiratorie	5,5
Varicella	Aerotrasportato	3,7-5
Morbillo	Aerotrasportato	12-18

Per ogni agente infettivo, la letteratura scientifica potrebbe riportare numerosi valori R₀ diversi.

R₀ si basa necessariamente su semplificazioni e dipende da moltissimi fattori, in parte imprevedibili (es.: congiunzione con un terremoto, un evento meteorologico o socioeconomico, una crisi umanitaria o una guerra).

La scelta dei modelli (e dei parametri inseriti) influenza i risultati, che possono differire sensibilmente in studi diversi.

Tale discrepanza è normale e può avere 3 motivi:

1. Le variabili considerate differiscono;
2. I metodi di modellazione differiscono;
3. Le procedure di stima differiscono.

Le stime del valore di R₀ sono spesso calcolate in funzione di 3 parametri primari:

1. la durata della contagiosità dopo l'infezione di una persona;
2. la probabilità di infezione per contatto tra una persona sensibile e una persona infettiva o un vettore;
3. il tasso di contatto,

insieme con parametri accessori che possono essere aggiunti per descrivere cicli di trasmissione più complessi.

Provvedimenti sociali e di sanità pubblica influenzano le dinamiche di trasmissione e quindi sono rilevanti per la stima dei valori di R₀.

Tuttavia, anche se l'infettività di un patogeno (cioè la probabilità di infezione che si verifica dopo che si è verificato un contatto efficace) e la durata della contagiosità sono costanti biologiche, R₀ varierà se le interazioni sociali variano nel tempo o nello spazio. Qualsiasi fattore che potrebbe influenzare il tasso di contatto, compresa la densità di popolazione (ad es. rurale vs. urbano), l'organizzazione sociale (ad es. integrata vs. segregata) e la stagionalità (ad es. stagione umida vs. piovosa per infezioni trasmesse da vettori), alla fine influenza l'R₀. Poiché R₀ è una funzione dell'effettivo tasso di contatto, il valore di R₀ è una funzione del comportamento e dell'organizzazione sociale umana, nonché delle caratteristiche biologiche innate degli agenti patogeni.

La stima del R₀ presuppone che il numero di infezioni secondarie prodotte da un singolo caso sia costante. In realtà alcuni agenti patogeni, come i virus, possono mutare e diventare più o meno contagiosi e/o pericolosi. Ci sono poi soggetti che sono superinfettori ed eventi di super-propagazione, in cui un singolo soggetto, magari asintomatico, può infettare un grande numero di persone.

La variabilità nelle stime del valore di R₀ per malattie infettive può essere molto ampia. Più di 20 diversi valori di R₀ (da 5,4 a 18) sono stati riportati per il morbillo. Sempre in merito al morbillo, una revisione del 2017, ha identificato stime di R₀ fatte su dati rilevati localmente che vanno da 3,7 a 203,3.

Nessun modello può prendere in considerazione tutta l'eterogeneità spazio-temporale di un contesto eco-epidemiologico, o anche il grado di trasmissibilità o vulnerabilità alle infezioni. Inoltre, nel mondo reale, il numero riproduttivo di base viene costantemente modificato durante l'epidemia, in particolare dalle misure di contenimento, di controllo adottate o imposte proprio per ridurlo.

Modelli per il calcolo del R₀ di una epidemia

Simulazione della diffusione epidemica di un modello SIR con R₀=8
Blu=suscettibili
Celeste=infetti
Marrone=recuperati

Contare il numero di casi di infezione durante un'epidemia può essere estremamente difficile, anche quando i funzionari della sanità pubblica usano la sorveglianza attiva e la ricerca dei contatti per tentare di localizzare tutte le persone infette. Sebbene sia possibile misurare il tasso d'attacco e il tasso d'attacco secondario riferiti a uno specifico periodo temporale, il valore di R₀ è quasi sempre stimato dai dati sieroepidemiologici o utilizzando modelli matematici teorici.

Sono quasi cento anni che si usano modelli matematici per descrivere la dinamica delle epidemie. Infatti i modelli attualmente usati in gran parte originano dal modello proposto da Kermack e McKendrick nel 1927. I modelli matematici più utilizzati necessitano di classificare la popolazione in compartimenti:

• $S$, suscettibili
• $I$, infetti / infettivi
• $E$, esposti, quando ad esempio la malattia richiede due settimane per rendere l'individuo infettivo
• $D$, deceduti
• $R$, recuperati, guariti dopo aver contratto la malattia
• $R$, rimossi, soggetti non infettabili perché immuni o isolati
• $M$, soggetti con immunità o infettività dalla nascita, materna
• $C$, soggetti portatori (carrier) asintomatici
• $H$, soggetti ospedalizzati
• $Q$, soggetti in quarantena

Per completare i modelli matematici si devono stimare alcuni parametri: età di infezione, cioè da quanto tempo è passato dal contagio, infettività, frequenza di contatto, periodo di incubazione, periodo infettivo, intervallo seriale, cioè il tempo fra la comparsa dei sintomi in un infetto e la comparsa dei sintomi in un individuo infettato dal primo, e altri parametri ricavati sul campo. Si deve anche definire la legge secondo cui si infettano i suscettibili. I modelli più semplici utilizzano la legge di azione di massa (sistema omogeneo) dove si assume che ogni individuo abbia la stessa probabilità di contattare qualunque altro individuo nella popolazione, indipendentemente dai contatti passati. La maggioranza dei modelli matematici viene denotata da un acronimo che rappresenta il flusso dell'epidemia tra i diversi compartimenti di popolazione.

• SI : $S\Longrightarrow I$
• SIS : $S\Longrightarrow I\Longrightarrow S$
• SIR : $S\Longrightarrow I\Longrightarrow R$
• SEIR : $S\Longrightarrow E\Longrightarrow I\Longrightarrow R$
• MSIR : $M\Longrightarrow S\Longrightarrow I\Longrightarrow R$
• MSEIR : $M\Longrightarrow S\Longrightarrow E\Longrightarrow I\Longrightarrow R$

I modelli possono adattarsi a malattie infettive nella fase epidemica o endemica, a sistema aperto (considerando nascite e morti) o chiuso. I modelli più semplici permettono di ricavare R₀ da una serie di equazioni differenziali mentre nei modelli più complessi si deve ricorrere al calcolo matriciale. I modelli, deterministici (che producono gli stessi risultati ogni volta che vengono eseguiti) o stocastici (che generano una distribuzione di risultati probabili sulla base delle variazioni degli input) danno R₀ diversi.

Calcolo della massima percentuale possibile di infetti

Il numero di riproduzione di base nei modelli epidemiologici dove la proporzione di suscettibili è pari al 100% e l'immunità acquisita dai guariti è definitiva permette di determinare la percentuale massima possibile di persone infette in una data popolazione. Prendendo ad esempio un modello SEIR, Indichiamo la proporzione totale di tutte le persone infette, $j(t):=e(t)+i(t)$, applicato al sistema di equazioni del modello SEIR

${\begin{aligned}s(t)&=-\beta {\frac {SI}{N}},\\e(t)&=\beta {\frac {SI}{N}}-aE,\\i(t)&=aE-\gamma I,\\r(t)&=\gamma I.\end{aligned}}$

da cui segue l'equazione differenziale${\frac {\mathrm {d} j}{\mathrm {d} s}}={\frac {\mathrm {d} e+\mathrm {d} i}{\mathrm {d} s}}={\frac {-\gamma i+\beta si}{-\beta si}}={\frac {\gamma }{\beta s}}-1$

essendo $R_{0}={\frac {\beta }{\gamma }}$

si ha

$j(t)+s(t)-{\frac {1}{R_{0}}}\ln s(t)=j(0)+s(0)-{\frac {1}{R_{0}}}\ln s(0)$

essendo $ln$ il logaritmo naturale da cui

$j_{\text{max}}=j(0)+s(0)-{\frac {1}{R_{0}}}\ln s(0)-{\frac {1}{R_{0}}}+{\frac {1}{R_{0}}}\ln {\frac {1}{R_{0}}}=j(0)+s(0)+{\frac {1}{R_{0}}}\left(\ln {\frac {1}{R_{0}s(0)}}-1\right).$

considerando una infezione con un nuovo virus avendo s(0) uguale a 1 e j(0) = 0 si può ricavare il numero massimo di infetti funzione di R0

$j_{\text{max}}=1+{\frac {1}{R_{0}}}\left(\ln {\frac {1}{R_{0}}}-1\right).$

Calcolo del R₀ basato sull'età media degli infettati

Esiste un caso particolare in cui R₀ può essere stimato senza utilizzare sistemi di equazioni differenziali. Una malattia infettiva è endemica se continua a esistere all'interno di una popolazione senza influenze esterne. Ciò significa che in media ogni persona malata ne infetta esattamente un'altra. Se questo valore fosse inferiore, la malattia si estinguerebbe, se fosse più grande, si svilupperebbe in un'epidemia a causa della crescita esponenziale. Matematicamente parlando, questo significa:

$R_{0}\cdot S=1$ essendo $S$ la quota di suscettibili rispetto alla popolazione totale.

Affinché una malattia con un elevato numero riproduttivo di base rimanga endemica, il numero di persone che sono effettivamente suscettibili deve essere necessariamente piccolo.

In una popolazione con piramide dell'età rettangolare si può presumere che ogni individuo della popolazione abbia esattamente la stessa aspettativa di vita. Se l'età media degli infettabili, le persone più giovani sono sensibili, mentre le persone anziane sono già state immunizzate (o sono ancora infettive) da una precedente infezione. Di conseguenza, la percentuale di coloro che sono infettabili è:

$S={\frac {A}{L}}$ essendo $L$ l'età media della popolazione e $A$ l'età media degli infettati.

Nel caso endemico, tuttavia, vale anche:

$S={\frac {1}{R_{0}}}$

Quindi questo vale

${\frac {1}{R_{0}}}={\frac {A}{L}}\qquad \Rightarrow \qquad R_{0}={\frac {L}{A}}$

che consente una stima del numero di riproduzione di base facilmente determinabile.

Nel caso in cui la piramide dell'età della popolazione sia esponenziale, si devono utilizzare modelli basati su sistemi di equazioni differenziali ordinarie con cui determinare l'equilibrio endemico da cui si ricava:

$R_{0}=1+{\frac {L}{A}}$

Calcolo di R₀ con periodo infettivo latente e con isolamento dopo la diagnosi

Durante un'epidemia, in genere il numero di infezioni diagnosticate col tempo è conosciuto. Nelle prime fasi di un'epidemia, la crescita è esponenziale, con un tasso di crescita logaritmico

$K={\frac {d\ln(P)}{dt}}$

dove $P$ può essere interpretato come il numero cumulativo di diagnosi (compresi gli individui che si sono ripresi) o il numero attuale di pazienti positivi; il tasso di crescita logaritmica è lo stesso per entrambe le definizioni. Per stimare $R_{0}$ sono necessarie ipotesi sul ritardo tra l'infezione e la diagnosi e il tempo che intercorre tra l'infezione e l'infettività.

Un modello più realistico per calcolare il numero di riproduzione di base in una epidemia dove vengono assunte misure di contenimento, come l'isolamento dei diagnosticati positivi, considera quindi anche i seguenti parametri:

• un individuo è infetto, ma non ha sintomi e non infetta ancora gli altri entra nel compartimento $E$. La durata dello stato esposto è $\tau _{E}$.
• un individuo è infetto, non ha sintomi, ma infetta gli altri. La durata dello stato infettivo latente è $\tau _{I}$. L'individuo infetta altre persone durante questo periodo.
• Se per prevenire ulteriori infezioni nelle misure di contenimento viene disposto l'isolamento dopo la diagnosi positiva: gli individui isolati, se l'isolamento è efficace, rientrano tra i rimossi $R$.

In questo caso si può utilizzare un modello SEIR e R₀ può essere scritto nella seguente forma:

$R_{0}=1+K(\tau _{E}+\tau _{I})+K^{2}\tau _{E}\tau _{I}.$

$K$ può essere calcolato considerando l'equazione differenziale per il numero di soggetti esposti $n_{E}$ e il numero dei soggetti infettivi nel periodo di latenza $n_{I}$

${\frac {d}{dt}}{\begin{pmatrix}n_{E}\\n_{I}\end{pmatrix}}={\begin{pmatrix}-1/\tau _{E}&R_{0}/\tau _{I}\\1/\tau _{E}&-1/\tau _{I}\end{pmatrix}}{\begin{pmatrix}n_{E}\\n_{I}\end{pmatrix}}.$

$K$ è il più grande autovalore della matrice, cioè, essendo $f={\frac {\tau _{I}}{\tau _{E}+\tau _{I}}}$ allora $K={\frac {-1+\surd [(1-2f)^{2}+4f(1-f)R_{0}]}{\frac {2f(1-f)\tau _{I}}{\tau _{I}+\tau _{E}}}}$ da cui è possibile ricavare $R_{0}$.

Numero di riproduzione netto al tempo t

La definizione del numero di riproduzione netto al tempo $t$, chiamato $R_{t}$ (dizione: erre con t), è analoga a quella di $R_{0}$, con la differenza che $R_{t}$ viene calcolato in un preciso momento. L' $R_{t}$ può essere anche chiamato: numero di riproduzione effettivo ($R_{e}$) o numero di riproduzione real-time o numero di riproduzione corrente ($R_{c}$).

La variazione di $R_{t}$ nel tempo permette di monitorare l'evoluzione di una epidemia e l’efficacia degli interventi adottati per contenerla.

Come $R_{0}$, $R_{t}$ può essere calcolato a partire dal numero di nuovi casi giornalieri. $R_{t}$ e $R_{0}$ variano entrambi a seconda delle dinamiche sociali di una popolazione: anche un virus facilmente trasmissibile avrà difficoltà a diffondersi in una popolazione dove le persone si incontrano raramente.

La stima di $R_{t}$ viene effettuata con relativamente complessi metodi statistici applicati al modello matematico che meglio descrive l'andamento dell'epidemia.

Esistono due definizioni principali dell'$R_{t}$, a volte chiamate: $R_{t}istantaneo$ e $R_{t}caso$ o di coorte. Considerando un'epidemia dove abbiamo un intervento efficace per contenerla e il numero di nuovi casi giornalieri ha smesso di crescere, l'$R_{t}istantaneo$ al momento in cui sono stati adottati i provvedimenti di contenimento dell'epidemia, viene calcolato partendo dal presupposto che il futuro non sia noto, mentre l'$R_{t}caso$ è calcolato utilizzando i dati dei giorni successivi. La distinzione tra $R_{t}istantaneo$ e $R_{t}caso$ è simile alla distinzione tra la durata della vita effettiva degli individui nati nel 2013, che possiamo misurare solo retrospettivamente dopo che tutti gli individui sono morti, e l'aspettativa di vita nel 2013, stimata ora ma supponendo che i tassi di mortalità in futuro saranno simili a quelli del 2013. L'$R_{t}istantaneo$ può essere stimato dal rapporto tra il numero di nuove infezioni generate alla fase temporale t e la totale contagiosità degli individui infetti al tempo t , espressa da $w_{s}$, profilo di infettività nel tempo di chi viene infettato. $R_{t}istantaneo$ è il numero medio di casi secondari che ogni individuo infetto infetterebbe se le condizioni rimanessero come erano al tempo t.

$R_{t}caso$ è il numero medio di casi secondari che un caso infettato alla fase temporale t finirà per infettare. La stima di $R_{t}caso$ può essere fatta solo a posteriori, una volta che sono stati infettati i casi secondari generati dai casi infetti al tempo t.

Calcolo del R_t

Nel corso di una epidemia Il calcolo dell'$R_{t}$, in particolare dell'$R_{t}istantaneo$, può essere un importante ausilio al processo decisionale sulle misure da prendere per contenerla, anche se l'utilizzo dell'$R_{t}$ come principale indicatore della gravità dell'epidemia può essere controverso.

Sono stati sviluppati vari metodi di calcolo dell'$R_{t}$ basati per lo più sul modello SEIR dove nel compartimento $I$ (infetti/infettivi) normalmente non si calcolano gli asintomatici, dipendendo questi dal numero di test fatti per rilevarli.

Una delle formule più utilizzate, inserita anche in alcuni pacchetti software per l'epidemiologia considera:

$R_{t}={\frac {I_{t}}{\displaystyle \sum _{s=1}^{t}w_{s}I_{t-s}}}$

dove $I_{t}$ è il numero di infezioni avvenute nel giorno t e $w_{s}$ è l'intervallo di generazione o seriale, cioè la probabilità che ci siano $s$ giorni tra quando un soggetto viene contagiato e quando contagia un nuovo soggetto. Dopo che una persona è stata infettata, la sua infettività dura un certo numero di giorni (in genere: dopo un periodo di latenza, aumenta rapidamente, quindi diminuisce gradualmente), quindi l'intervallo di generazione è una distribuzione di probabilità. Anche un $R_{t}$ di 1,3 con un tempo di generazione di 4 giorni significa un raddoppio del numero di nuovi casi entro circa 11 giorni.

Il metodo di calcolo utilizzato dall'Istituto Superiore di Sanità nel corso dell'epidemia di COVID-19 si basa sull’utilizzo di un più complesso metodo Monte Carlo su catena di Markov, che sfrutta quindi un campionamento effettivo della distribuzione di probabilità con un numero sufficientemente alto di input calcolati passo passo (la catena di Markov). Dopo un certo numero di passi, l'algoritmo converge verso la miglior distribuzione descrittiva dell'evoluzione dell'epidemia.

A tal fine l'algoritmo deve essere applicato ad una funzione di verosimiglianza, che fornisca un metodo per poter aiutare l’algoritmo nella ricerca della corretta distribuzione. Il valore di questa funzione di verosimiglianza viene definito in base ai valori ottenuti nel comportamento dell'epidemia in una finestra temporale antecedente.

La funzione di verosimiglianza applicata dall'ISS è :

${L}=\prod _{t=1}^{T}P(C_{t}-Imp_{t}|R_{t}{\displaystyle \sum _{s=1}^{t}w_{s}C_{t-s}})$

con

· $P(k|\lambda )$ è la densità di una distribuzione Poisson, ovvero la probabilità di osservare k eventi se questi avvengono a una frequenza media λ.

· $C_{t}$ è il numero di casi sintomatici con data di inizio sintomi al giorno t, con t=1,…,T

· $Imp_{t}$ è il numero di casi sintomatici importati da un’altra regione o dall’estero aventi di data inizio sintomi nel giorno t

· $w_{s}$ è la distribuzione dell'intervallo di generazione (una distribuzione gamma con parametri di shape α = 1.87 e rate β = 0.28, stimata su dati della Regione Lombardia tra febbraio e marzo del 2020).

Incertezze e variabilità

La stima di $R_{t}$ prodotta è un intervallo di credibilità, di solito al 95%. Questo vuol dire che il modello fornisce una probabilità del 95% che il valore di $R_{t}$ si trovi all’interno dell’intervallo.

Visto che l'$R_{t}$, in un certo contesto geografico, una volta nota la distribuzione dell’intervallo di generazione (ovvero la distanza temporale fra la comparsa dei sintomi in una persona infettata e i casi da essa generati) può essere stimato a partire dalla data di contagio ricavata per lo più dall'anamnesi fatta alla data di inizio dei sintomi, la stima soffre di un ritardo temporale di giorni o settimane. I ritardi nelle segnalazioni nella sorveglianza della malattia compromettono la capacità di valutare l'effettiva dinamica di un'epidemia. Si deve allora stimare il ritardo nei tempi di segnalazione (nowcasting) che può essere di giorni o settimane. Inoltre la stima riporta valori mediati sia su base spaziale che temporale. Un singolo focolaio, limitato nel tempo e nello spazio, innalza il valore medio giornaliero di una intera regione. Anche per ridurre la variabilità giornaliera dei dati, usualmente nel processo decisionale sulle misure da adottare per contenere una epidemia si utilizzano medie mobili come ad esempio: $R_{t}medio14gg$.

Voci correlate

• Modelli matematici in epidemiologia
• Tasso di letalità
• Tasso d'attacco
• Tasso netto di riproduzione#R0 nei modelli epidemici
• Immunità di gregge

Altri progetti

Altri progetti

• Wikimedia Commons

• Wikimedia Commons contiene immagini o altri file su numero di riproduzione di base