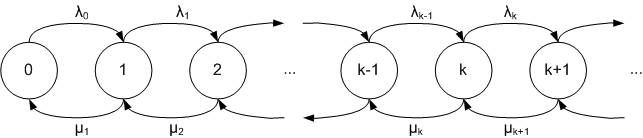
Processo di nascita e morte
Un processo di nascita e morte è un processo stocastico markoviano a tempo continuo sullo spazio degli stati dato dall'insieme dei numeri naturali, che simula l'andamento di una popolazione i cui unici cambiamenti siano le nascite e le morti. In altre parole, se il processo si trova in uno stato n, può solamente passare o allo stato n+1 (nascita) o allo stato n-1 (morte). I processi di nascita e morte hanno importanti applicazioni in biologia, teoria delle code e demografia.
Definizione
modificaUn processo di nascita e morte è un processo stocastico su che soddisfa le seguenti proprietà:
- Gli incrementi sono indipendenti, ossia la quantità di passaggi di stato in intervalli disgiunti sono indipendenti tra loro.
- Se il processo si trova in n, la probabilità di una nascita in un piccolo intervallo di tempo è proporzionale alla lunghezza dell'intervallo, ossia per
- Se il processo si trova in n>0, la probabilità di una morte in un piccolo intervallo di tempo è proporzionale alla lunghezza dell'intervallo, ossia per
- Se il processo si trova in n, la probabilità che il processo si allontani per più di due stati è trascurabile, ossia per
Le quantità λn e μn sono i coefficienti di natalità e di mortalità.
Proprietà
modifica- Il processo soddisfa la proprietà di Markov.
- Il processo soddisfa la proprietà di Markov forte.
- La probabilità che il processo resti nello stesso stato in un piccolo intervallo di tempo è data, per , da
- Il tempo di attesa tra un passaggio di stato e il successivo ha legge esponenziale di parametro (λn + μn).
- Il processo di Poisson è un caso particolare di processo di nascita e morte nel caso in cui μn=0 e λn=λ per ogni n.
Condizioni per la ricorrenza e la transitorietà
modificaLe condizioni per la ricorrenza e la transitorietà sono state stabilite da Samuel Karlin e James McGregor.[1].
Un processo di nascita e morte è ricorrente se e solo se
Un processo di nascita e morte è ergodico se e solo se
Un processo di nascita e morte è nullo-ricorrente se e solo se
Le condizioni per la ricorrenza, la transitorietà, l'ergodicità e la ricorrenza nulla possono essere derivate in una forma più esplicita[2].
Per ogni intero , sia la -esima iterazione del logaritmo naturale, ossia , e per qualsiasi , .
Quindi, le condizioni per la ricorrenza e la transitorietà di un processo di nascita e morte sono le seguenti.
Il processo di nascita e morte è transitorio se esistono , e , tale che per ogni si ha
dove la somma vuota per si assume che sia 0.
Il processo di nascita e morte è ricorrente se esistono e , tali che per ogni si ha
Possono essere trovate classi più ampie di processi di nascita e morte per i quali è possibile stabilire le condizioni per la ricorrenza e la transitorietà[3].
Applicazione
modificaConsideriamo il passeggiata aleatoria unidimensionale , , che è definito come segue. Lasciare e , , dove accetta valori , e la distribuzione di è definito dalle seguenti condizioni:
dove soddisfano la condizione , .
- Il passeggiata aleatoria qui descritto è un analogo a tempo discreto del processo di nascita e morte (vedi catena di Markov) con i tassi di natalità
- e i tassi di mortalità
Quindi, la ricorrenza o la transitorietà del passeggiata aleatoria è associata alla ricorrenza o alla transitorietà del processo di nascita e morte.[2]
- La passeggiata aleatoria è transitorio se esiste , e tale che per ogni
- dove la somma vuota per è assunto pari a zero.
La passeggiata aleatoria è ricorrente se esiste e tale che per ogni
Note
modifica- ^ Karlin, Samuel e McGregor, James, The classification of birth and death processes (PDF), in Transactions of the American Mathematical Society, vol. 86, n. 2, 1957, pp. 366–400, DOI:10.1090/S0002-9947-1957-0094854-8.
- ^ a b Vyacheslav M. Abramov, Extension of the Bertrand–De Morgan test and its application, in The American Mathematical Monthly, vol. 127, n. 5, 2020, pp. 444–448, DOI:10.1080/00029890.2020.1722551, arXiv:1901.05843.
- ^ Vyacheslav M. Abramov, Necessary and sufficient conditions for the convergence of positive series (PDF), in Journal of Classical Analysis, vol. 19, n. 2, 2022, pp. 117–125, DOI:10.7153/jca-2022-19-09, arXiv:2104.01702.
Bibliografia
modifica- Samuel Karlin e Howard M. Taylor, A first course in stochastic processes, Academic Press, 1975.