Distribuzione esponenziale

In teoria delle probabilità la distribuzione esponenziale è una distribuzione di probabilità continua che descrive la "durata di vita" di un fenomeno che non invecchia (ossia la distribuzione esponenziale è priva di memoria). Un esempio è la durata di vita di una particella radioattiva prima di decadere oppure la durata della richiesta di un servizio; dunque essa è in relazione al tempo di attesa del primo successo, in fenomeni aleatori con distribuzione geometrica.

Distribuzione esponenziale ${\mathcal {E}}(\lambda )$
Funzione di densità di probabilità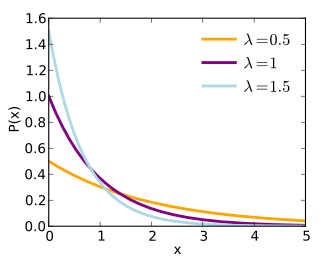
Funzione di ripartizione
Parametri	$\lambda >0\$
Supporto	$\mathbb {R} ^{+}$
Funzione di densità	$\lambda e^{-\lambda x}\$
Funzione di ripartizione	$1-e^{-\lambda x}\$
Valore atteso	${\frac {1}{\lambda }}\$
Mediana	${\frac {\log(2)}{\lambda }}$
Moda	$0\$
Varianza	${\frac {1}{\lambda ^{2}}}$
Indice di asimmetria	$2\$
Curtosi	$6\$
Entropia	$1-\log(\lambda )\$
Funzione generatrice dei momenti	$\left(1-{\frac {t}{\lambda }}\right)^{-1}$
Funzione caratteristica	$\left(1-{\frac {it}{\lambda }}\right)^{-1}$

La distribuzione esponenziale (o di Laplace) può dedursi anche come la distribuzione di probabilità di una variabile aleatoria definita come somma dei quadrati di due variabili aleatorie normali standardizzate (ossia con valore atteso zero e varianza unitaria); dunque è banalmente riconducibile anche a un caso particolare di distribuzione del chi-quadro, essendo, quest'ultima, la distribuzione di probabilità della variabile aleatoria costruita come la somma dei quadrati di n variabili aleatorie indipendenti normali e standardizzate.

Definizione

La distribuzione esponenziale ${\mathcal {E}}(\lambda )$, con parametro $\lambda >0$, ha funzione di densità di probabilità:

$f(x;\lambda )={\begin{cases}\lambda e^{-\lambda x}&x>0,\\0&x\leq 0.\end{cases}}$

Proprietà

Il parametro $\lambda$ dev'essere positivo affinché l'integrale della funzione di densità sui reali sia $1.$

Assenza di memoria

Una variabile aleatoria $X$ con distribuzione esponenziale di parametro $\lambda$ ha funzione di ripartizione

$F(x)=P(X\leqslant x)=1-e^{-\lambda x}.$

In particolare la formula $P(X>x)=e^{-\lambda x}$ implica la mancanza di memoria:

$P(X>a+b|X>a)={\frac {P(X>a+b)}{P(X>a)}}=P(X>b).$

Viceversa, se una distribuzione di probabilità continua sui numeri reali positivi è priva di memoria, ovvero rispetta ${P(X>a+b)=P(X>a)P(X>b)}$ per ogni scelta di $a$ e di $b,$ allora vale la relazione $P(X>x)=P(X>1)^{x}$ per ogni $x$ razionale positivo o persino, grazie alla continuità della funzione di ripartizione, per ogni $x$ reale positivo; in particolare prendendo $\lambda =-\log P(X>1)$ si trova proprio

$F(x)=1-P(X>x)=1-e^{-\lambda x}.$

Fra le distribuzioni di probabilità discrete, invece, ogni distribuzione priva di memoria è una distribuzione geometrica.

Caratteristiche

Una variabile aleatoria con distribuzione esponenziale di parametro $\lambda$ ha

• valore atteso $E[X]=1/\lambda$,
• varianza ${\text{Var}}(X)=1/\lambda ^{2}$,
• funzione caratteristica $\phi _{X}(t)=\left(1-{\frac {it}{\lambda }}\right)^{-1}$
• funzione generatrice dei momenti $g_{X}(t)=\left(1-{\frac {t}{\lambda }}\right)^{-1}$
• indici di asimmetria e di curtosi $\gamma _{1}=2$ e $\gamma _{2}=6$.
• generici momenti centrali $\mu _{n}={\frac {1}{\lambda ^{n}}}!n={\lambda }^{-n}n!\sum _{k=0}^{n}(-1)^{k}/k!={\frac {\Gamma (n+1,-1)}{e\lambda ^{n}}}$ dove $!n$ è il sub-fattoriale di $n$.

I suoi quantili si possono ricavare invertendo la funzione di ripartizione:

$\alpha =F(q_{\alpha })=1-e^{-\lambda q_{\alpha }}$

$q_{\alpha }=F^{-1}(\alpha )={\frac {1}{\lambda }}\log {\frac {1}{1-\alpha }}$;

in particolare i suoi quartili (e la mediana) sono

$q_{1/4}={\frac {1}{\lambda }}\log {\frac {4}{3}}$, $q_{1/2}={\frac {1}{\lambda }}\log 2$, $q_{3/4}={\frac {1}{\lambda }}\log 4$.

Distribuzioni

Il minimo $Y=\min\{X_{1},\dots ,X_{n}\}$ tra $n$ variabili aleatorie indipendenti con distribuzioni esponenziali di parametri $\lambda _{1},\dots ,\lambda _{n}$ è ancora una variabile aleatoria con distribuzione esponenziale, di parametro $\lambda =\lambda _{1}+\dots +\lambda _{n}$.

Il parallelo della distribuzione esponenziale, come distribuzione priva di memoria, tra le distribuzioni di probabilità discrete è la distribuzione geometrica. In particolare, se $X$ segue la distribuzione esponenziale ${\mathcal {E}}(\lambda )$ allora per ogni $\theta >0$ la variabile aleatoria $Y_{\theta }=[\theta X]$ (parte intera) segue la distribuzione geometrica ${\mathcal {G}}(e^{-\lambda /\theta })$:

$P(Y=n)=P(n\leqslant \theta X<n+1)=F_{X}\left({\frac {n+1}{\theta }}\right)-F_{X}\left({\frac {n}{\theta }}\right)=\left(1-e^{-\lambda /\theta }\right)\left(e^{-\lambda /\theta }\right)^{n}.$

La distribuzione di Poisson ${\mathcal {P}}(\lambda )$ descrive il numero di eventi successivi intercorsi in un intervallo di tempo, dove i tempi di attesa tra due eventi successivi sono indipendenti e regolati dalla distribuzione esponenziale di medesimo parametro $\lambda$.

La distribuzione esponenziale ${\mathcal {E}}\left({\tfrac {1}{2}}\right)$ corrisponde alla distribuzione chi quadrato con due gradi di libertà, $\chi ^{2}(2)$.

La distribuzione di Laplace di parametri $(\mu ,b)$ governa la variabile aleatoria $Y=\mu +X_{1}-X_{2}$, dove $X_{1},X_{2}$ sono due variabili aleatorie indipendenti con la medesima distribuzione esponenziale ${\mathcal {E}}(1/b)$.

La distribuzione Gamma generalizza la distribuzione esponenziale: $\Gamma (1,\lambda )$ coincide con ${\mathcal {E}}(\lambda )$. In particolare, la somma $Y=X_{1}+\dots +X_{n}$ di $n$ variabili aleatorie indipendenti di medesima legge esponenziale con parametro $\lambda$ segue la distribuzione Gamma $\Gamma (n,\lambda )$. Inoltre nell'inferenza bayesiana se il parametro $\lambda$ di una distribuzione esponenziale segue, a priori di un'osservazione, una distribuzione Gamma, allora segue una distribuzione Gamma anche a posteriori.

Applicazioni

Radioattività

Il tempo di decadimento di un isotopo radioattivo viene solitamente modellato in funzione della sua vita media tramite la distribuzione esponenziale ${\mathcal {E}}(1/\tau )$.

In questo quadro il parametro $\lambda =1/\tau$ è detto costante di decadimento; la speranza di vita è proprio $E[X]=1/\lambda =\tau$.

Con questo modello si possono ad esempio calcolare le probabilità che l'isotopo decada in meno della metà del tempo medio,

$P(T<{\tfrac {1}{2}}\tau )=F({\tfrac {1}{2}}\tau )=1-e^{-\lambda {\frac {1}{2}}\tau }=1-e^{-{\frac {1}{2}}}\approx 0,393$,

o in più del doppio di questo tempo

$P(T>2\tau )=1-F(2\tau )=e^{-\lambda \tau }=e^{-2}\approx 0,135$.

Tramite la formula per i quantili si trova ad esempio che solo con probabilità di un ventesimo l'isotopo decadrà in più di

$q_{1-1/20}={\tfrac {1}{\lambda }}\log 20\approx 3\tau$.

Ciononostante un osservatore che non abbia ancora visto decadere l'isotopo dopo un tempo di $3\tau$ si ritrova nuovamente nelle condizioni iniziali, a causa dell'assenza di memoria; dovrà quindi aspettare mediamente un tempo $\tau$ prima del decadimento.

In un campione con un numero di isotopi molto grande (come avviene solitamente), le probabilità di ogni singolo isotopo (indipendente dagli altri) si possono tradurre in percentuali del campione. Ad esempio, il tempo medio dopo il quale metà dei campioni decadono (emivita o tempo di dimezzamento) è dato dalla mediana $q_{1/2}=(\log 2)/\lambda$.

Voci correlate

• Decadimento esponenziale
• Distribuzione geometrica
• Distribuzione di Poisson
• Funzione esponenziale
• Mancanza di memoria

Altri progetti

Altri progetti

• Wikimedia Commons

• Wikimedia Commons contiene immagini o altri file su distribuzione esponenziale

Collegamenti esterni

• (EN) exponential distribution, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
• (EN) Eric W. Weisstein, Distribuzione esponenziale, su MathWorld, Wolfram Research.

Controllo di autorità	GND (DE) 4016019-1