Interazione di Fermi
In fisica delle particelle, l'interazione di Fermi (o anche la teoria di Fermi del decadimento beta o l'interazione a quattro fermioni di Fermi) è una spiegazione del decadimento beta proposta da Enrico Fermi nel 1933.[1] La teoria postula che quattro fermioni interagiscano tra loro direttamente (in un vertice del diagramma di Feynman associato). Questa interazione spiega il decadimento beta di un neutrone tramite l'accoppiamento diretto di un neutrone con un elettrone, un neutrino (poi determinato essere un antineutrino) e un protone.[2]
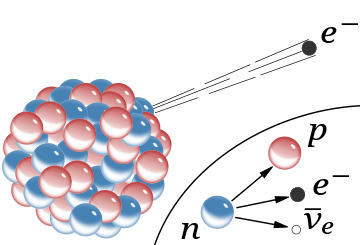
Fermi introdusse per la prima volta questo accoppiamento nella sua descrizione del decadimento beta nel 1933.[3] L'interazione di Fermi è antecedente alla teoria dell'interazione debole, dove l'interazione tra il protone–neutrone e l'elettrone–antineutrino è mediata da un bosone W− virtuale, della quale la teoria di Fermi è la teoria di campo efficace a basse energie.
Storia dell'iniziale rifiuto e della successiva pubblicazione modifica
La prima rivista scientifica alla quale Fermi inviò il suo «tentativo» di teoria del decadimento beta fu la prestigiosa Nature, che tuttavia rifiutò la pubblicazione «perché conteneva speculazioni troppo distanti dalla realtà per essere interessanti al lettore».[4] Fermi quindi inviò delle versioni rivisitate dell'articolo a pubblicazioni italiane e tedesche, che accettarono e pubblicarono il lavoro nelle loro lingue nel 1933 e nel 1934.[5][6][7] L'articolo non appariva all'epoca in una rivista primaria in inglese. Una traduzione inglese di questo articolo seminale fu pubblicata nell'American Journal of Physics nel 1968.[8] Nature avrebbe in seguito ammesso che quel rifiuto sia stato uno dei più grandi errori editoriali della sua storia.[9]
Fermi si sentì tanto turbato dall'iniziale rifiuto del suo articolo che decise di lasciare per un po' la fisica teorica e dedicarsi solo alla fisica sperimentale. Questo avrebbe portato poco tempo dopo al suo famoso lavoro con l'attivazione dei nuclei tramite neutroni lenti.
Il «tentativo» modifica
Definizioni modifica
La teoria tratta di tre tipi di particelle che si presumono essere in interazione diretta: inizialmente una “particella pesante” nello “stato neutronico” ( ), che poi transisce nel suo “stato protonico” ( ) con l'emissione di un elettrone e di un neutrino.
Stato elettronico modifica
dove è la funzione d'onda di un singolo elettrone e sono i suoi stati stazionari.
è l'operatore che distrugge un elettrone nello stato che agisce nello spazio di Fock come
è il corrispondente operatore di creazione:
Stato neutrinico modifica
Analogamente si definisce la funzione d'onda di singolo neutrino,
e da
e gli operatori di distruzione che agisce sullo spazio di Fock come
mentre è il corrispondente operatore di creazione.
Stato di particella pesante modifica
è l'operatore introdotto da Heisenberg (poi generalizzato nell'isospin) che agisce su uno stato di particella pesante, che ha autovalore +1 quando la particella è un neutrone e −1 quando è un protone. Quindi, gli stati di particella pesante saranno rappresentati da vettori colonna con due righe, dove
rappresenta un neutrone, e
rappresenta un protone (nella rappresentazione dove è l'usuale matrice di spin ).
Gli operatori che trasformano una particella pesante da un protone a un neutrone e viceversa sono rispettivamente rappresentati da
L'hamiltoniana è composta di tre parti: , rappresentante l'energia delle particelle pesanti libere, , rappresentante l'energia delle particelle leggere libere, e una parte che dà l'interazione .
( ) è un'autofunzione per un neutrone (protone) nello stato .
Hamiltoniana modifica
dove e sono rispettivamente gli operatori di energia del neutrone e del protone, cosicché se , , e se , .
dove è l'energia dell'elettrone nello stato -esimo nel campo di Coulomb del nucleo, e è il numero di elettroni in quello stato; è il numero di neutrini nello stato -esimo e è l'energia di ciascun neutrino in (che si assume essere in uno stato libero, di onda piana).
La parte di interazione deve contenere un termine che rappresenta la trasformazione di un protone in un neutrone insieme all'emissione di un elettrone e un neutrino (in realtà antineutrino), nonché un termine per il processo inverso; la forza di Coulomb tra l'elettrone e il protone viene trascurata poiché irrilevante per il processo di decadimento .
Fermi propose due valori possibili per : dapprima, una versione non relativistica che ignora lo spin:
e successivamente una versione che assume che le particelle leggere siano spinori di Dirac a quattro componenti, ma che la velocità delle particelle pesanti è piccola rispetto a e che i termini di interazione analoghi al potenziale vettore elettromagnetico possono essere ignorati:
dove ora e sono spinori di Dirac a quattro componenti, rappresenta il coniugato hermitiano di , e è la matrice
Elementi di matrice modifica
Lo stato del sistema si assume dato dalla ennupla dove specifica se la particella pesante è un neutrone o un protone, è lo stato quantistico della particella pesante, è il numero di elettroni nello stato e è il numero di neutrini nello stato .
Usando la versione relativistica di , Fermi dà l'elemento di matrice tra lo stato con un neutrone nello stato e nessun elettrone (neutrino) presente nello stato ( ), e lo stato con un protone nello stato e un elettrone e un neutrino presente negli stati e come
dove l'integrale viene fatto su tutto lo spazio delle configurazione delle particelle pesanti (eccetto per ). Il segno è determinato a seconda se il numero totale delle particelle sia dispari (−) o pari (+).
Influenze modifica
Poco dopo la pubblicazione dell'articolo di Fermi, Werner Heisenberg fece notare in una lettera a Wolfgang Pauli[10] che l'emissione e l'assorbimento dei neutrini e degli elettroni nel nucleo dovrebbe, al secondo ordine in teoria delle perturbazioni, portare all'attrazione tra i protoni e i neutroni, analogamente a come l'emissione e l'assorbimento dei fotoni portano alla forza elettromagnetica. Trovò che la forza sarebbe della forma , ma che il valore sperimentale del tempo portava a un valore che era troppo piccola di un fattore di un milione.[11]
L'anno seguente, Hideki Yukawa elaborò questa idea,[12] ma nella sua teoria i neutrini e gli elettroni sono stati sostituiti da una nuova particella ipotetica con una massa a riposo circa 200 volte maggiore di quella dell'elettrone (il pione).[13]
Sviluppi successivi modifica
La teoria a quattro fermioni di Fermi descrive l'interazione debole sorprendentemente bene. Tuttavia, la sezione d'urto calcolata, ovvero la probabilità di interazione, cresce con il quadrato dell'energia: , dove GF è la costante di Fermi, che indica la forza dell'interazione. Siccome la sezione d'urto cresce senza limite, la teoria non è valida a energie molto maggiori di 100 GeV, cioè nel cosiddetto limite ultravioletto (UV). Questo ha implicato la necessità di raffinare la teoria trovando un suo completamento UV, riconosciuto nella teoria elettrodebole, in cui l'interazione dei quattro fermioni a contatto è sostituita dallo scambio a distanza di un bosone W o Z.
L'interazione potrebbe anche spiegare il decadimento del muone tramite un accoppiamento di un muone, elettrone-antineutrino, muone-neutrino e elettrone, con la stessa forza fondamentale dell'interazione. Questa ipotesi fu proposta da Gershtein e Zeldovich ed è nota come l'ipotesi di conservazione di corrente vettoriale.[14]
Nella teoria originale, Fermi assunse che la forma di interazione è un accoppiamento di contatto di due correnti vettoriali. Successivamente, Lee e Yang evidenziarono che niente impediva la presenza di una corrente assiale che viola la parità, e questo fu confermato dall'esperimento di Wu.[15][16]
L'inclusione della violazione di parità nell'interazione di Fermi fu fatta da George Gamow e Edward Teller nelle cosiddette transizioni di Gamow-Teller che descrivono l'interazione di Fermi in termini di decadimenti che violano la parità "permessi" e decadimenti che conservano la parità "superpermessi" in termini di stati di spin dell'elettrone e del neutrino rispettivamente antiparalleli e paralleli. Prima dello sviluppo della teoria elettrodebole e del modello standard, George Sudarshan e Robert Marshak e indipendentemente Richard Feynman e Murray Gell-Mann, riuscirono a determinare la corretta struttura tensoriale (vettore meno vettore assiale, V − A) dell'interazione a quattro fermioni.[17][18]
Costante di Fermi modifica
La determinazione più precisa della costante di Fermi viene dalle misure del tempo di vita del muone, che è inversamente proporzionale al quadrato di GF (quando si trascura la massa del muone rispetto alla massa del bosone W).[19] In termini moderni:[3][20]
dove g è la costante di accoppiamento dell'interazione debole, e MW è la massa del bosone W, che media il decadimento in questione.
Nel modello standard, la costante di Fermi è correlata al valore di aspettazione del vuoto di Higgs
- .[21]
Più direttamente, (al tree level per il modello standard),
Questo può essere ulteriormente semplificato in termini dell'angolo di Weinberg usando la relazione tra i bosoni W e Z con , cosicché
Note modifica
- ^ C. N. Yang, Fermi's β-decay Theory, in Asia Pacific Physics Newsletter, vol. 1, n. 1, 2012, pp. 27-30, DOI:10.1142/s2251158x12000045.
- ^ R.P. Feynman, Theory of Fundamental Processes, W. A. Benjamin, 1962, Capitoli 6 & 7.
- ^ a b David J. Griffiths, Introduction to Elementary Particles, 2ª ed., 2009, pp. 314-315, ISBN 978-3-527-40601-2.
- ^ Abraham Pais, Inward Bound, Oxford, Oxford University Press, 1986, p. 418, ISBN 0-19-851997-4.
- ^ E. Fermi, Tentativo di una teoria dei raggi β, in La Ricerca Scientifica, vol. 2, n. 12, 1933.
- ^ E. Fermi, Tentativo di una teoria dei raggi β, in Il Nuovo Cimento, vol. 11, n. 1, 1934, pp. 1-19, Bibcode:1934NCim...11....1F, DOI:10.1007/BF02959820.
- ^ (DE) E. Fermi, Versuch einer Theorie der beta-Strahlen. I, in Zeitschrift für Physik, vol. 88, 1934, p. 161, Bibcode:1934ZPhy...88..161F, DOI:10.1007/BF01351864.
- ^ F. L. Wilson, Fermi's Theory of Beta Decay, in American Journal of Physics, vol. 36, n. 12, 1968, pp. 1150-1160, Bibcode:1968AmJPh..36.1150W, DOI:10.1119/1.1974382. Comprende la traduzione completa in inglese dell'articolo di Fermi in tedesco del 1934.
- ^ Frank Close, Neutrino[collegamento interrotto], Oxford University Press, 23 febbraio 2012.
- ^ Wolfgang Pauli, Scientific Correspondence with Bohr, Einstein, Heisenberg a.o. Volume II:1930–1939, Springer-Verlag Berlin Heidelberg GmbH, 1985, p. 250, lettera #341, Heisenberg a Pauli, 18 gennaio 1934.
- ^ Laurie M Brown, The Origin of the Concept of Nuclear Forces, Institute of Physics Publishing, 1996, Section 3.3.
- ^ (EN) H. Yukawa, On the interaction of elementary particles. I., in Proceedings of the Physico-Mathematical Society of Japan, vol. 17, 1935, p. 1.
- ^ Jagdish Mehra, The Historical Development of Quantum Theory, Volume 6 Part 2 (1932–1941), Springer, 2001, p. 832.
- ^ S. S. Gerstein e Ya. B. Zeldovich, Meson corrections in the theory of beta decay, in Zh. Eksp. Teor. Fiz., 1955, pp. 698-699.
- ^ T. D. Lee e C. N. Yang, Question of Parity Conservation in Weak Interactions, in Physical Review, vol. 104, n. 1, 1956, pp. 254-258, Bibcode:1956PhRv..104..254L, DOI:10.1103/PhysRev.104.254.
- ^ C. S. Wu, E Ambler e R. W. Hayward, Experimental Test of Parity Conservation in Beta Decay, in Physical Review, vol. 105, n. 4, 1957, pp. 1413-1415, Bibcode:1957PhRv..105.1413W, DOI:10.1103/PhysRev.105.1413.
- ^ R. P. Feynman e M. Gell-Mann, Theory of the Fermi interaction (PDF), in Physical Review, vol. 109, n. 1, 1958, p. 193, Bibcode:1958PhRv..109..193F, DOI:10.1103/physrev.109.193.
- ^ E. C. Sudarshan e R. E. Marshak, Chirality invariance and the universal Fermi interaction, in Physical Review, vol. 109, n. 5, 1958, p. 1860, Bibcode:1958PhRv..109.1860S, DOI:10.1103/physrev.109.1860.2.
- ^ D. B. Chitwood e MuLan Collaboration, Improved Measurement of the Positive-Muon Lifetime and Determination of the Fermi Constant, in Physical Review Letters, vol. 99, n. 3, 2007, p. 032001, Bibcode:2007PhRvL..99c2001C, DOI:10.1103/PhysRevLett.99.032001, PMID 17678280, arXiv:0704.1981.
- ^ Fermi coupling constant, su physics.nist.gov. URL consultato il 31 ottobre 2016.
- ^ T. Plehn e M. Rauch, Quartic Higgs coupling at hadron colliders, in Physical Review D, vol. 72, n. 5, 2005, p. 053008, Bibcode:2005PhRvD..72e3008P, DOI:10.1103/PhysRevD.72.053008, arXiv:hep-ph/0507321.