Trasversalità
In matematica, e più precisamente in topologia differenziale, la trasversalità è una proprietà opposta alla tangenza. Viene definita nel contesto di curve, superfici o più generali varietà differenziabili contenute in un qualche spazio.
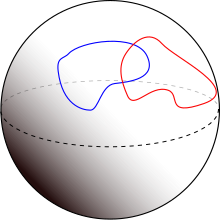

La nozione di trasversalità fa uso del calcolo infinitesimale (in particolare, dello spazio tangente).
Definizione
modificaDue sottovarietà differenziabili di una varietà differenziabile M di dimensione n si intersecano in modo trasverso in un punto x se i due spazi tangenti corrispettivi in quel punto generano lo spazio tangente ad M nel punto x.
Nel caso in cui le sottovarietà abbiano dimensioni complementari (cioè la cui somma è n), questo equivale a chiedere che i due sottospazi tangenti siano in somma diretta, ovvero che si intersechino solamente in un punto (questo segue dalla formula di Grassmann).
Proprietà
modificaL'intersezione di due varietà trasverse è anch'essa una varietà, la cui codimensione è pari alla somma delle codimensioni delle due varietà di partenza (quando non è vuota). Entrambe queste proprietà dipendono dalla trasversalità: se l'intersezione di due varietà non è trasversa, l'intersezione può non essere una varietà, e se è una varietà può comunque avere dimensione arbitraria.
In particolare, due varietà con dimensioni complementari si intersecano in punti isolati. Se una delle due varietà è compatta, questi punti sono finiti. Se le due varietà e la varietà ambiente sono tutte orientate, ciascun punto di intersezione ha un segno + o -. La somma di questi segni è una quantità importante in topologia algebrica, perché non cambia se una delle due varietà è spostata tramite una isotopia.
Due varietà la cui somma delle dimensioni è minore della dimensione n della varietà ambiente sono trasverse se e solo se non si intersecano. Infatti in questo caso gli spazi tangente hanno dimensione troppo piccola e non possono in nessun caso generare uno spazio di dimensione n.
Più in generale, secondo la definizione, due varietà che non si intersecano sono comunque trasverse.
Voci correlate
modificaCollegamenti esterni
modifica- (EN) Eric W. Weisstein, Trasversalità, su MathWorld, Wolfram Research.