Prisma

Il prisma in geometria solida è un poliedro le cui basi sono due poligoni congruenti di n lati posti su piani paralleli e connessi da un ciclo di parallelogrammi (le "facce laterali").

Prisma
Forma facce	2 n-goni, n parallelogrammi
Nº facce	2 + n
Nº spigoli	3n
Nº vertici	2n
Valenze vertici	3
Duale	Dipiramide
Proprietà	convesso
Sviluppo piano

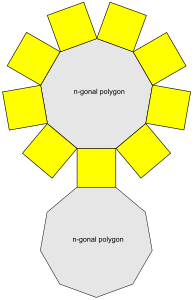Nomenclatura

Le basi

Se il poligono che forma le basi è un particolare poligono, ad esempio un triangolo, quadrato, pentagono, etc. si parla rispettivamente di "prisma triangolare", "prisma quadrato", '"pentagonale", etc. In generale, si parla di "prisma n-gonale".

Prismi retti e obliqui

Se le facce laterali sono tutte dei rettangoli il poliedro è un "prisma retto": in questo caso infatti le facce laterali formano degli angoli retti con entrambe le basi. In caso contrario si parla di "prisma obliquo".

Prisma retto (A) e obliquo (B)

Parallelepipedi

Un prisma che ha tutte le facce a forma di parallelogramma è un parallelepipedo. Si tratta, quindi, di un prisma le cui basi sono parallelogrammi.

Prismi regolari

Un "prisma regolare" è un prisma retto la cui base è un poligono regolare.

Proprietà

Prismi

Dualità

Il poliedro duale di un prisma è una bipiramide.

Volume

Il volume di un prisma è dato dal prodotto dell'area di una delle sue basi per la distanza tra i piani (paralleli) ai quali appartengono. Se il prisma è retto, questa distanza è pari alla lunghezza di uno spigolo verticale (altrimenti no).

Simmetrie

Un prisma regolare con $n\neq 4$ lati ha $4n$ simmetrie. Per $n=4$ il prisma regolare è in realtà un cubo e le simmetrie sono di più (48), perché è possibile scambiare una faccia laterale con una base.

Più precisamente, il gruppo di simmetria di un prisma regolare con $n\neq 4$ lati è il prodotto diretto $D_{2n}\times \mathbb {Z} /_{2\mathbb {Z} }$ del gruppo diedrale di ordine $2n$ con il gruppo ciclico di ordine 2. Il gruppo diedrale rappresenta infatti tutte le simmetrie che preservano ciascuna base, ed è quindi isomorfo al gruppo $D_{2n}$ di simmetrie di un $n$-gono regolare, mentre il secondo fattore rappresenta l'isometria che scambia le due basi.

Voci correlate

Modelli di prisma triangolare, pentagonale ed eptagonale

• Antiprisma
• Piramide

Altri progetti

Altri progetti

• Wikizionario
• Wikimedia Commons

• Wikizionario contiene il lemma di dizionario «prisma»
• Wikimedia Commons contiene immagini o altri file sul prisma

Collegamenti esterni

• Prisma, su Treccani.it – Enciclopedie on line, Istituto dell'Enciclopedia Italiana.
• Arturo Maroni, PRISMA, in Enciclopedia Italiana, Istituto dell'Enciclopedia Italiana, 1935.
• Prisma, in Dizionario delle scienze fisiche, Istituto dell'Enciclopedia Italiana, 1996.
• Prisma, su Vocabolario Treccani, Istituto dell'Enciclopedia Italiana.
• prisma, su sapere.it, De Agostini.
• Prisma, in Enciclopedia della Matematica, Istituto dell'Enciclopedia Italiana, 2013.
• (EN) Eric W. Weisstein, Prism, su MathWorld, Wolfram Research.
• (EN) Prism, su Encyclopaedia of Mathematics, Springer e European Mathematical Society.
• (EN) Modelli cartacei di prismi e antiprismi, su software3d.com.
• (EN) The Uniform Polyhedra di Roman Mäder
• (EN) Virtual Reality Polyhedra, su georgehart.com.