Distribuzione di Erlang
In teoria delle probabilità la distribuzione di Erlang è una distribuzione di probabilità continua con supporto e caratterizzata dai seguenti due parametri:
- un intero positivo (in inglese shape);
- un reale positivo detto tasso.
| Distribuzione di Erlang | |
|---|---|
Funzione di densità di probabilità 
| |
Funzione di ripartizione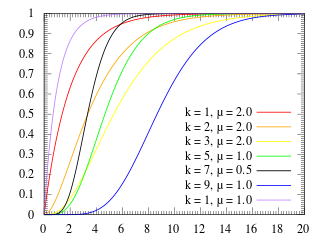
| |
| Parametri | , tasso (reale) |
| Supporto | |
| Funzione di densità | |
| Funzione di ripartizione | |
| Valore atteso | |
| Moda | |
| Varianza | |
| Indice di asimmetria | |
| Curtosi | |
| Entropia | |
| Funzione generatrice dei momenti | per |
| Funzione caratteristica | |
La distribuzione di Erlang (di rado distribuzione k-Erlang) con parametro unitario si semplifica in una distribuzione esponenziale. Infatti tale distribuzione può essere considerata come la somma di variabili aleatorie indipendenti e identicamente distribuite secondo un'esponenziale di parametro . La distribuzione di Erlang è anche un caso particolare di una distribuzione Gamma la quale prevede, generalmente, un parametro reale. Ponendo invece la distribuzione diventa una distribuzione chi quadrato con gradi di libertà.
La distribuzione di Erlang fu sviluppata da A. K. Erlang per esaminare il numero di chiamate telefoniche che gli operatori di un centralino possono ricevere nello stesso istante. Questo lavoro di analisi del traffico fu applicato anche nella teoria delle code per descrivere i tempi di attesa. Oggi è usata principalmente nell'ambito dei processi stocastici e delle scienze matematiche applicate alla biologia.
Caratteristiche
modificaFunzione di densità di probabilità
modificaLa funzione di densità di probabilità di una distribuzione di Erlang è:
Per la presenza del fattoriale al denominatore, la distribuzione di Erlang è definita esclusivamente per valori di interi e positivi. La distribuzione Gamma generalizza quella di Erlang per valori reali di utilizzando la funzione Gamma generale invece del fattoriale.
Funzione di ripartizione
modificaLa funzione cumulativa della distribuzione di Erlang è:
dove appartiene all'insieme delle funzioni gamma incomplete. La funzione di ripartizione può essere anche espressa nel seguente modo:
Proprietà
modificaSoluzione equazione differenziale
modificaLa distribuzione di Erlang è soluzione della seguente equazione differenziale:
con condizione iniziale .
Somma di variabili casuali con distribuzione esponenziale
modificaLa distribuzione k-Erlang è la distribuzione di probabilità della somma di variabili casuali con distribuzione esponenziale con identico parametro:
- se allora
Mediana
modificaRiguardo alla mediana di una distribuzione di Erlang si conosce il comportamento asintotico, i quali coefficienti possono essere calcolati computazionalmente. Un'approssimazione è:
- con media [1]
Generazione numeri casuali distribuiti secondo una Erlang
modificaPer generare un numero casuale secondo una distribuzione di Erlang, si generino numeri distribuiti secondo una uniforme standard ( ) e si usi la seguente formula[2]:
Eventi stocastici
modificaTempi d'attesa
modificaL'occorrenza di eventi indipendenti aventi un certo tasso medio viene modellizata con un processo di Poisson. Poiché in un processo di Poisson gli intertempi tra un evento ed il successivo sono distribuiti esponenzialmente, il tempo di attesa per osservare la realizzazione di eventi è distribuito secondo una .
La distribuzione di Erlang (un classico uso di questa distribuzione è l'uso per misurare il tempo tra chiamate telefoniche), può essere utilizzata in combinazione col valore atteso delle durate delle chiamate in modo tale da avere informazioni riguardo al traffico di telefonate (misurato, infatti, in Erlang). Ciò viene utilizzato per calcolare la probabilità di perdere telefonate o di far attendere dei clienti al telefono, in base alle ipotesi di rifiuto di chiamate (formula di Erlang B) o di messa in coda (formula di Erlang C).
Distribuzioni associate
modificaLa distribuzione di Erlang è legata alle seguenti distribuzioni:
- se allora con ;
- (distribuzione normale);
- se e allora ;
- se numero reale, si ottiene una (distribuzione Gamma);
- (distribuzione esponenziale);
- (distribuzione chi quadrato);
- se e allora (distribuzione di Pareto).
Note
modifica- ^ Banneheka BMSG, Ekanayake GEMUPD (2009) "A new point estimator for the median of gamma distribution". Viyodaya J Science, 14:95-103
- ^ http://www.xycoon.com/erlang_random.htm
Bibliografia
modifica- Ian Angus "An Introduction to Erlang B and Erlang C", Telemanagement #187 (PDF Document - Has terms and formulae plus short biography)
Voci correlate
modificaCollegamenti esterni
modifica


















