Poliedro composto
In geometria solida si chiama poliedro composto o composto poliedrico una figura geometrica formata da due o più poliedri che condividono un baricentro comune.
Ad ogni composto poliedrico sono associate due particolari caratteristiche che individuano due nuovi poliedri ad esso correlati:
– la chiusura convessa di un composto è il più piccolo poliedro convesso che lo contiene;
– l'intersezione o nucleo di un composto è la porzione di spazio comune a tutti i suoi componenti.
Si deduce facilmente che il nucleo di un composto poliedrico è esso stesso un poliedro ed in particolare che è un poliedro convesso se tutti i componenti sono convessi.
La chiusura convessa è detta anche, in maniera del tutto equivalente, inviluppo convesso oppure involucro convesso.
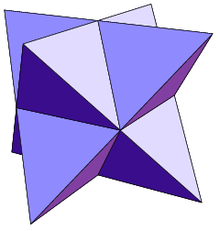
Un esempio di composto poliedrico è la stella ottangola mostrata in figura: essa è un composto di due tetraedri regolari ed ha come chiusura convessa un cubo e come nucleo un ottaedro.
Composti regolari
modificaUn composto poliedrico si dice regolare se soddisfa le normali condizioni di regolarità che valgono anche per i poliedri semplici (non composti) ossia deve essere omogeneo nei vertici, negli spigoli e nelle facce: cioè per ogni coppia di vertici (o di spigoli o di facce) esiste una simmetria del poliedro che trasforma uno dei due elementi nel secondo.
Risulta evidente perciò che affinché un composto sia regolare è necessario – ma non sufficiente – che tutti i suoi componenti siano regolari ed eguali tra loro. Più nello specifico i componenti saranno esclusivamente tetraedri, ottaedri o cubi.
Esistono in tutto 5 poliedri composti regolari (ovvero 6 se si considerano le due forme chirali di uno come due poliedri distinti). Sono elencati di seguito:
| componenti | figura | elementi
notevoli |
inviluppo | intersezione | simmetrie | duale |
|---|---|---|---|---|---|---|
| 2 tetraedri | |
V = 8
S = 12 F = 8 |
cubo | ottaedro | 48
gruppo Oh |
sé stesso |
| 5 cubi | V = 20
S = 60 F = 30 |
dodecaedro | triacontaedro | 120
gruppo Ih |
5 ottaedri | |
| 5 ottaedri | V = 30
S = 60 F = 40 |
icosidodecaedro | icosaedro | 120
gruppo Ih |
5 cubi | |
| 5 tetraedri
(chirale) |
V = 20
S = 30 F = 20 |
dodecaedro | icosaedro | 60
gruppo I |
5 tetraedri
speculari | |
| 10 tetraedri | V = 20
S = 60 F = 40 |
dodecaedro | icosaedro | 120
gruppo Ih |
sé stesso |
I gruppi e sono rispettivamente il gruppo di simmetria dell'ottaedro e dell'icosaedro. Il gruppo è il sottogruppo in dato dalle simmetrie che preservano l'orientazione.
Il poliedro duale del composto di cinque tetraedri è l'immagine riflessa di sé stesso; l'unione dei due forma il composto di dieci tetraedri.
Composti uniformi
modificaUna caratteristica meno restrittiva rispetto alla regolarità è quella di uniformità, che include tutti i composti con vertici omogenei, le cui facce siano poligoni regolari. Ciò implica che i componenti debbano essere essi stessi uniformi e congruenti tra loro.
Una classificazione completa di tutti i possibili composti uniformi fu fornita da John Skilling nel 1976. L'elenco enumera 75 elementi, indicati con la sigla UC (uniform compound) seguita da un indice numerico. Vi sono inclusi i 5 composti regolari, 20 composti non banali di prismi ed antiprismi, 2 classi infinite di prismi e 4 classi infinite di antiprismi. Alcuni dei composti uniformi hanno un grado di libertà rotazionale, cioè l'inclinazione dei componenti è variabile, pur mantenendo inalterate le simmetrie del composto.
- Esempi di composti poliedrici uniformi
-
12 tetraedri UC02 (rotazione libera)
-
4 ottaedri UC12
-
20 ottaedri UC13 (rotazione libera)
-
10 ottaedri UC15 (primo tipo)
-
10 ottaedri UC16 (secondo tipo)
-
2n antiprismi di basi {p/q} con q dispari UC22
-
4 prismi triangolari UC30 (chirale)
-
6 prismi stellati pentagonali UC36 (chirale)
-
4 prismi esagonali UC38
-
6 prismi decagonali UC40
-
3 antiprismi quadrati UC42
-
2 icosaedri UC46
-
5 icosaedri UC47
-
5 piccoli dodecaedri stellati UC51
-
5 tetraedri troncati UC55 (chirale)
-
5 cubottaedri UC59
-
2 cubi simi (speculari) UC68
Il composto di 20 ottaedri con libertà rotazionale (UC13) presenta 4 casi particolari, classificati con codici distinti: il composto regolare di 5 ottaedri (UC17), due differenti composti di 10 ottaedri (UC15 e UC16) ed un composto di 20 ottaedri "fisso" con vertici a due a due coincidenti (UC14).
I poliedri uniformi chirali (simi, camusi, retrocamusi e camusi invertiti) formano naturalmente un composto poliedrico uniforme se sovrapposti alla propria immagine riflessa. Rientra in questa categoria – pur non essendo chirale – anche l'icosaedro, considerato come un "tetraedro simo".
Non vi è alcun caso di composto poliedrico uniforme costituito da dodecaedri platonici, né da grandi dodecaedri stellati.
Bibliografia
modifica- H. M. Cundy & A. P. Rollett, I modelli matematici, Milano, Feltrinelli, 1974.
- Maria Dedò, Forme, simmetria e topologia, Bologna, Decibel & Zanichelli, 1999, ISBN 88-08-09615-7.
- Skilling John, Uniform Compounds of Uniform Polyhedra, Mathematical Proceedings of the Cambridge Philosophical Society, 1976, DOI:10.1017/S0305004100052440.
Voci correlate
modificaAltri progetti
modifica- Wikimedia Commons contiene immagini o altri file su poliedro composto
Collegamenti esterni
modifica- Modelli in carta dei poliedri, su korthalsaltes.com.
- The 75 Uniform Compounds of Uniform Polyhedra, su interocitors.com. Modelli grafici 3D di composti ad orientamento variabile.